1.
如图,点 是以
是以 为直径的半圆上一点,连接
为直径的半圆上一点,连接 , 点
, 点 是
是 上一个动点,连接
上一个动点,连接 , 作
, 作 交
交 于点
于点 , 交半圆于点
, 交半圆于点 . 已知:
. 已知: , 设
, 设 的长度为
的长度为 ,
,  的长度为
的长度为 ,
,  的长度为
的长度为 (当点
(当点 与点
与点 重合时,
重合时, ,
,  , 当点
, 当点 与点
与点 重合时,
重合时, ,
,  ).
).
小锐同学根据学习函数的经验,分别对函数 ,
随自变量
变化而变化的规律进行了探究.


下面是小锐同学的探究过程,请补充完整:
(1)
按照下表中自变量 的值进行取点、画图、测量,分别得到了
的值进行取点、画图、测量,分别得到了 ,
,  与
与 的几组对应值,请补全表格:
的几组对应值,请补全表格:
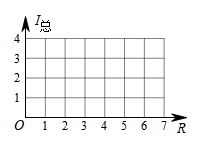
(2)
在同一平面直角坐标系 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点 ,
,  , 并画出函数
, 并画出函数 ,
,  的图象(
的图象( 已经画出);
(3)
结合函数图象解决问题:①当
已经画出);
(3)
结合函数图象解决问题:①当 ,
,  的长都大于
的长都大于 时,
时, 长度的取值范围约是;(精确到0.1);②继续在同一坐标系中画出所需的函数图象,判断点
长度的取值范围约是;(精确到0.1);②继续在同一坐标系中画出所需的函数图象,判断点 ,
,  ,
,  能否在以
能否在以 为圆心的同一个圆上?(填“能”或“否”)
为圆心的同一个圆上?(填“能”或“否”)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 8.00 | 5.81 | 4.38 | 3.35 | 2.55 | 1.85 | 1.21 | 0.60 | 0.00 |
| 0.00 | 0.90 | 2.24 | 2.67 | 2.89 | 2.83 | 2.34 | 0.00 |
上表中.(精确到0.1)
【考点】
函数值;
描点法画函数图象;
通过函数图象获取信息;
能力提升