1.
在数学兴趣小组活动中,小明同学对几何动点问题进行了探究:
问题背景:在中,
. 点D为
边上一动点,连接
, 点
为
边上一动点,连接
, 以
为边,在
右侧作等边
, 连接
.

(1)
如图1,当 时,求证:
时,求证: ;
(2)
如图2,当点
;
(2)
如图2,当点 运动到
运动到 的四等分点(靠近点
的四等分点(靠近点 )时,点
)时,点 停止运动,此时点
停止运动,此时点 从点
从点 运动到点
运动到点 , 试判断点
, 试判断点 从点
从点 运动到点
运动到点 的过程中线段
的过程中线段 和
和 的数量关系,并说明理由;
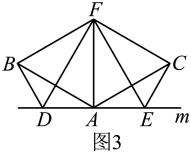
(3)
如图3,点
的数量关系,并说明理由;
(3)
如图3,点 从
从 的四等分点(靠近点
的四等分点(靠近点 )出发,向终点A运动,同时,点
)出发,向终点A运动,同时,点 从点
从点 出发,向终点
出发,向终点 运动,运动过程中,始终保持
运动,运动过程中,始终保持 , 求出
, 求出 的最小值.
的最小值.
【考点】
三角形全等的判定;
线段垂直平分线的性质;
等腰三角形的性质;
等边三角形的判定与性质;
三角形全等的判定-SAS;