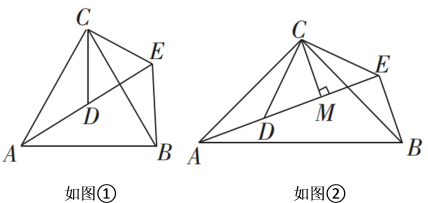
问题呈现：阿基米德折弦定理：如图1，和是的两条弦（即折线是圆的一条折弦），， M是的中点，则从M向所作垂线的垂足D是折弦的中点，即．下面是运用“截长法”证明的部分证明过程．

0 返回出卷网首页

1. 问题呈现：阿基米德折弦定理：如图1， $\text{[math]}$ 和 $\text{[math]}$ 是 $\text{[math]}$ 的两条弦（即折线 $\text{[math]}$ 是圆的一条折弦）， $\text{[math]}$ ， M是 $\text{[math]}$ 的中点，则从M向 $\text{[math]}$ 所作垂线的垂足D是折弦 $\text{[math]}$ 的中点，即 $\text{[math]}$ ．下面是运用“截长法”证明 $\text{[math]}$ 的部分证明过程．

(1) 证明：如图2，在 $\text{[math]}$ 上截取 $\text{[math]}$ ，连接 $\text{[math]}$ 和 $\text{[math]}$ ．

∵M是 $\text{[math]}$ 的中点，∴ $\text{[math]}$ ……

请按照上面的证明思路，写出该证明的剩余部分；

(2) 实践应用：如图3，已知 $\text{[math]}$ 内接于 $\text{[math]}$ ， $\text{[math]}$ ， D是 $\text{[math]}$ 的中点，依据阿基米德折弦定理可得图中某三条线段的等量关系为．

(3) 如图4，已知等腰 $\text{[math]}$ 内接于 $\text{[math]}$ ， $\text{[math]}$ ， D为 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 于点E， $\text{[math]}$ 的周长为 $\text{[math]}$ ， $\text{[math]}$ ，请求出 $\text{[math]}$ 的长．

【考点】

三角形全等的判定-SAS; 解直角三角形—边角关系; 阿基米德折弦定理模型;

【答案】

您现在未登录，无法查看试题答案与解析。登录

实践探究题普通

1. 问题发现：如图①， $\text{[math]}$ 和 $\text{[math]}$ 均为等边三角形，点A、D、E在同一直线上，连结 $\text{[math]}$ ．填空：

(1) $\text{[math]}$ 的度数为；

(2) 线段 $\text{[math]}$ 之间的数量关系是．

(3) 拓展探究：

如图②， $\text{[math]}$ 和 $\text{[math]}$ 均为等腰直角三角形， $\text{[math]}$ ，点A，D，E在同一直线上， $\text{[math]}$ 为 $\text{[math]}$ 中 $\text{[math]}$ 边上的高，连结 $\text{[math]}$ ，请判断 $\text{[math]}$ 的度数及线段 $\text{[math]}$ 之间的数量关系，并说明理由．

实践探究题普通