如图发现问题小强在一次学习过程中遇到了下面的问题：如图①，已知AD 是△ABC 的中线，AB=6，AC=4，求AD的取值范围.

0 返回出卷网首页

1. 如图

发现问题

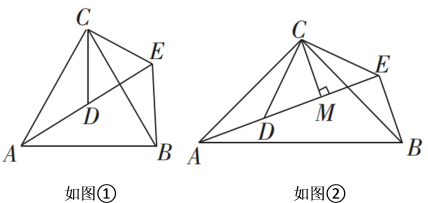
小强在一次学习过程中遇到了下面的问题：如图①，已知AD 是△ABC 的中线，AB=6，AC=4，求AD的取值范围.

(1) 探究方法

小强所在的小组通过探究发现，延长AD 至点E，使ED=AD.连接BE，可以证出△BED≌△CAD，利用全等三角形的性质可将已知的边长与 AD 转化到△ABE 中，进而求出AD的取值范围.

方法小结：从上面的思路可以看出，解决问题的关键是将中线AD 延长一倍，构造出全等三角形，我们把这种方法叫做“倍长中线法”.

请你利用上面解答问题的思路方法，写出求AD的取值范围的过程；

(2) 类比迁移

如图②，AD 是△ABC 的中线，在 AD 上取一点 E，连接BE 并延长交AC 于点 F，使AF=EF，求证：BE=AC；

(3) 拓展应用

如图③，在矩形ABCD中， $\text{[math]}$ 在 BD上取一点 F，以 BF 为斜边作 Rt△BEF，且 $\text{[math]}$ 点G是DF的中点，连接EG，CG.

求证：EG=CG.

【考点】

三角形三边关系; 三角形全等的判定-SAS; 倍长中线构造全等模型; 相似三角形的判定-SAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

实践探究题困难

1. 课外兴趣小组活动时，老师提出了如下问题：如图 1，在 $\text{[math]}$ 中，若 $\text{[math]}$ ，求 $\text{[math]}$ 边上的中线 $\text{[math]}$ 的取值范围．

小颖在组内经过合作交流，得到了如下的解决方法：如图 2，延长 $\text{[math]}$ 到点 $\text{[math]}$ ，使 $\text{[math]}$ ，连结 $\text{[math]}$ ．请根据小颖的方法思考：

(1) 由已知和作图能得到 $\text{[math]}$ ，依据是（） A. $\text{[math]}$ B. SAS C. AAS D. $\text{[math]}$

(2) 由 “三角形的三边关系” 可求得 $\text{[math]}$ 的取值范围是

(3) 解后反思：题目中出现 “中点” “中线”等条件，可考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形中．完成上题之后，小颖善于探究，她又提出了如下的问题，请你解答．

在 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 上一点，连结 $\text{[math]}$ 是 $\text{[math]}$ 上一点，连结 $\text{[math]}$ 并延长交边 $\text{[math]}$ 于点 $\text{[math]}$ ．如图 3，若 $\text{[math]}$ 是 $\text{[math]}$ 的中线，且 $\text{[math]}$ ，求证： $\text{[math]}$ ．

实践探究题普通

2. 问题发现：如图①， $\text{[math]}$ 和 $\text{[math]}$ 均为等边三角形，点A、D、E在同一直线上，连结 $\text{[math]}$ ．填空：

(1) $\text{[math]}$ 的度数为；

(2) 线段 $\text{[math]}$ 之间的数量关系是．

(3) 拓展探究：

如图②， $\text{[math]}$ 和 $\text{[math]}$ 均为等腰直角三角形， $\text{[math]}$ ，点A，D，E在同一直线上， $\text{[math]}$ 为 $\text{[math]}$ 中 $\text{[math]}$ 边上的高，连结 $\text{[math]}$ ，请判断 $\text{[math]}$ 的度数及线段 $\text{[math]}$ 之间的数量关系，并说明理由．

实践探究题普通