0 返回出卷网首页
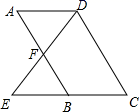
1. 已知平行四边形ABCD，E为BC边上的中点，F为AB边上的一点.

(1) 如图1，连接FE并延长交DC的延长线于点G，求证：FE=GE：
(2) 如图2，若FB+AB=DF，∠EDC=35°，求∠AFD：
(3) 如图3，若FE=DE，P为AF的中点，Q为FD的中点，AQ= ， DP=6，求线段BE的长.
【考点】
勾股定理; 平行四边形的性质; 三角形全等的判定-ASA; 四边形的综合; 全等三角形中对应边的关系;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 困难
能力提升
换一批
1. 如图，在▱ABCD中，AB＝AD，AC＝16，BD＝12，AC、BD相交于点O．

(1) 求AB的长．
(2) 若CE//BD，BE//AC，连接OE，求证：OE＝AD．
(3) 设BC与OE相交于点P，连接DP，求DP的长．
综合题 普通
2. 如图，四边形是平行四边形，延长至点 ， 使得 ， 连接交于点 ．

(1) 求证： ．
(2) 连接 ， 若 ， ， 求的长．
综合题 普通
3. 如图，四边形ABCD是平行四边形，延长CB至点E，使得BE＝BC，连结DE交AB于点F.

(1) 求证：△ADF≌△BEF.
(2) 连结DB，若AD＝DB＝5，CD＝6，求DE的长.
综合题 普通