1.
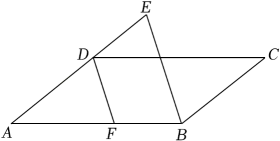
如图,在 中,
中, ,
,  ,
,  . 动点
. 动点 从点
从点 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿 向终点
向终点 运动,过点
运动,过点 作
作 交折线
交折线 于点
于点 , 以
, 以 为斜边向其右侧作等腰直角三角形
为斜边向其右侧作等腰直角三角形 . 设
. 设 与
与 重叠部分图形的面积为
重叠部分图形的面积为 , 点
, 点 的运动时间为
的运动时间为 秒
秒 .
.

(1)
点 到
到 的距离为________,
的距离为________, ________;
(2)
当点
________;
(2)
当点 落在线段
落在线段 上时,求
上时,求 的值;
(3)
求
的值;
(3)
求 与
与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围.
的取值范围.
【考点】
函数解析式;
等腰三角形的判定与性质;
平行四边形的性质;
求正切值;