1.
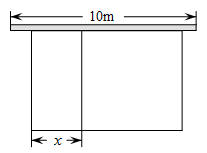
如图,利用一面墙(墙的长度不限),用 长的篱笆围成一个矩形
长的篱笆围成一个矩形 场地,若垂直于墙的一边
场地,若垂直于墙的一边 长为
长为 , 它的面积为
, 它的面积为 .
.

(1)
求矩形的面积 与
与 的函数关系式(要求写出自变量
的函数关系式(要求写出自变量 的取值范围);
(2)
当
的取值范围);
(2)
当 长为
长为 时,求矩形场地的面积.
时,求矩形场地的面积.
【考点】
一元二次方程的应用-几何问题;