1.
 的三边为
的三边为 ,
,  ,
,  , 定义:若其中两边平方和等于第三边平方的
, 定义:若其中两边平方和等于第三边平方的 倍(
倍( ,
,  为正整数),那么这个三角形叫做“
为正整数),那么这个三角形叫做“ 阶非凡三角形”.例如:当
阶非凡三角形”.例如:当 时,某三角形三边长分别是
时,某三角形三边长分别是 , 2和3,因为
, 2和3,因为 , 所以这个三角形是“3阶非凡三角形”.
, 所以这个三角形是“3阶非凡三角形”.
(1)
若 是“
是“ 阶非凡三角形”,三边长为
阶非凡三角形”,三边长为 , 4,
, 4, , 则
, 则 ______.
(2)
若
______.
(2)
若 是“2阶非凡三角形”(
是“2阶非凡三角形”( ),且
),且 ,
,  , 则
, 则 的长为______.
(3)
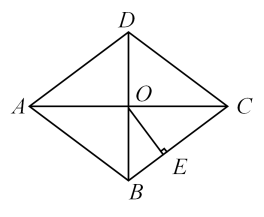
如图,在菱形
的长为______.
(3)
如图,在菱形 中,
中, 交
交 于点
于点 ,
,  , 且
, 且 是“3阶非凡三角形”
是“3阶非凡三角形” , 求
, 求 的值.
的值.

【考点】
二次根式的乘除法;
勾股定理;
菱形的性质;