1.
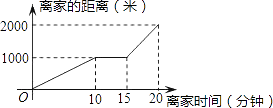
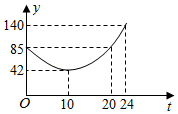
如图反映的过程是:小强从家去菜地浇水,又去玉米地除草,然后回家.如果菜地和玉米地的距离为a千米,小强在玉米地除草比在菜地浇水多用的时间为b分钟,则a,b的值分别为( )
A.
1.1,8
B.
0.9,3
C.
1.1,12
D.
0.9,8
【考点】
函数的图象;
分段函数;
基础巩固
能力提升
变式训练
拓展培优
真题演练