如图，菱形ABCD的边长为2，BD=2，E、F分别是边AD，CD上的两个动点，且满足AE+CF=2．

0 返回出卷网首页

1. 如图，菱形ABCD的边长为2，BD=2，E、F分别是边AD，CD上的两个动点，且满足AE+CF=2．

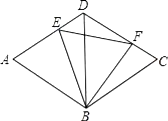
(1) 求证：△BDE≌△BCF；

(2) 判断△BEF的形状，并说明理由．

【考点】

三角形全等的判定; 等边三角形的判定与性质; 菱形的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，点D在 $\text{[math]}$ 内， $\text{[math]}$ ， $\text{[math]}$ ，点E在 $\text{[math]}$ 外， $\text{[math]}$ ， $\text{[math]}$ ．

(1) 判断 $\text{[math]}$ 的形状并加以证明．

(2) 连接DE，若 $\text{[math]}$ ， $\text{[math]}$ ，求DE的长．

综合题普通

2. 综合运用．

(1) 如图（ $\text{[math]}$ ），已知：在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，直线 $\text{[math]}$ 经过点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，垂足分别为点 $\text{[math]}$ ， $\text{[math]}$ ．证明： $\text{[math]}$ ．

(2) 如图（ $\text{[math]}$ ），将（ $\text{[math]}$ ）中的条件改为：在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点都在直线 $\text{[math]}$ 上，并且有 $\text{[math]}$ ，其中 $\text{[math]}$ 为任意锐角或钝角．请问结论 $\text{[math]}$ 是否成立？如成立，请你给出证明；若不成立，请说明理由．

(3) 拓展与应用：如图（ $\text{[math]}$ ）， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点所在直线 $\text{[math]}$ 上的两动点（ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点互不重合），点 $\text{[math]}$ 为 $\text{[math]}$ 平分线上的一点，且 $\text{[math]}$ 和 $\text{[math]}$ 均为等边三角形，连接 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，试判断 $\text{[math]}$ 的形状并说明理由．

综合题普通

3. 已知：△ABC和△ADE都是等边三角形，点D在BC边上，连接CE．

(1) 如图1，求证：BD＝CE；

(2) 如图2，点M在AC边上，且AM＝CD，连接EM交AB于点N，连接DM、DN，在不添加任何辅助线的情况下，请直接写出图2中四条与线段BD相等的线段（线段CE除外）

综合题普通