1.
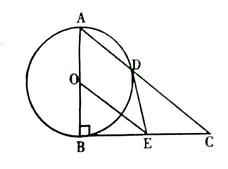
如图,以  的直角边
的直角边  为直径作
为直径作  交斜边
交斜边  于点
于点  ,过圆心
,过圆心  作
作  ,交
,交  于点
于点  ,连接
,连接  .
.
(1)
判断  与
与  的位置关系并说明理由;
(2)
求证:
的位置关系并说明理由;
(2)
求证:  ;
(3)
若
;
(3)
若  ,
,  ,求
,求  的长.
的长.
【考点】
全等三角形的判定与性质;
切线的判定与性质;
相似三角形的判定与性质;