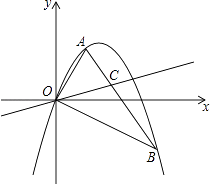
如图，抛物线y=ax2+bx经过△OAB的三个顶点，其中点A（1，），点B（3，﹣ ），O为坐标原点．

0 返回出卷网首页

1. 如图，抛物线y=ax²+bx经过△OAB的三个顶点，其中点A（1， $\text{[math]}$ ），点B（3，﹣ $\text{[math]}$ ），O为坐标原点．

(1) 求这条抛物线所对应的函数表达式；

(2) 若P（4，m），Q（t，n）为该抛物线上的两点，且n＜m，求t的取值范围；

(3) 若C为线段AB上的一个动点，当点A，点B到直线OC的距离之和最大时，求∠BOC的大小及点C的坐标．

【考点】

待定系数法求二次函数解析式; 二次函数与不等式（组）的综合应用; 二次函数图象上点的坐标特征; 二次函数的实际应用-几何问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 已知二次函数y=（x+1）（x+a）（其中a是常数）的图象经过点A（4，5），B（m，n），

(1) 求a的值；

(2) 求该抛物线的对称轴：

(3) 当n<5时，求m的取值范围。

综合题普通

2. 如图，抛物线 $\text{[math]}$ 与直线 $\text{[math]}$ 相交于 $\text{[math]}$ ， $\text{[math]}$ 两点，且抛物线经过点 $\text{[math]}$

(1) 求抛物线的解析式.

(2) 点P是抛物线上的一个动点（不与点 $\text{[math]}$ 点 $\text{[math]}$ 重合），过点P作直线 $\text{[math]}$ 轴于点D，交直线AB于点E.当 $\text{[math]}$ 时，求P点坐标；

(3) 如图所示，设抛物线与 $\text{[math]}$ 轴交于点F，在抛物线的第一象限内，是否存在一点Q，使得四边形OFQC的面积最大？若存在，请求出点Q的坐标；若不存在，说明理由.

综合题困难

3. 如图，抛物线y= $\text{[math]}$ x²+nx﹣2与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（﹣1，0）．

(1) 求抛物线的表达式；

(2) 在抛物线的对称轴上是否存在点P，使△PCD是直角三角形？如果存在，请直接写出点P的坐标，如果不存在，请说明理由；

(3) 点M是线段BC上的一个动点，过点M作x轴的垂线，与抛物线相交于点N，当点M移动到什么位置时，四边形CDBN的面积最大？求出四边形CDBN的最大面积及此时M点的坐标．

综合题困难