如图，平面直角坐标系中，点A、B、C在x轴上，点D、E在y轴上，OA=OD=2，OC=OE=4，B为线段OA的中点，直线AD与经过B、E、C三点的抛物线交于F、G两点，与其对称轴交于M，点P为线段FG上一个动点（与F、G不重合），PQ∥y轴与抛物线交于点Q．

0 返回出卷网首页

1. 如图，平面直角坐标系中，点A、B、C在x轴上，点D、E在y轴上，OA=OD=2，OC=OE=4，B为线段OA的中点，直线AD与经过B、E、C三点的抛物线交于F、G两点，与其对称轴交于M，点P为线段FG上一个动点（与F、G不重合），PQ∥y轴与抛物线交于点Q．

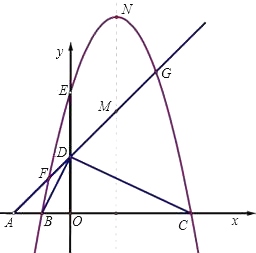
(1) 求经过B、E、C三点的抛物线的解析式；

(2) 判断△BDC的形状，并给出证明；当P在什么位置时，以P、O、C为顶点的三角形是等腰三角形，并求出此时点P的坐标；

(3) 若抛物线的顶点为N，连接QN，探究四边形PMNQ的形状：①能否成为菱形；

②能否成为等腰梯形？若能，请直接写出点P的坐标；若不能，请说明理由．

【考点】

待定系数法求二次函数解析式; 二次函数与一次函数的综合应用; 二次函数的实际应用-几何问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，抛物线 $\text{[math]}$ 交 $\text{[math]}$ 轴于 $\text{[math]}$ ， $\text{[math]}$ 两点，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，顶点为 $\text{[math]}$ ，对称轴分别交 $\text{[math]}$ 轴、 $\text{[math]}$ 于点 $\text{[math]}$ 、 $\text{[math]}$ ，点 $\text{[math]}$ 是射线 $\text{[math]}$ 上一动点，过点 $\text{[math]}$ 作 $\text{[math]}$ 的平行线 $\text{[math]}$ 交抛物线于点 $\text{[math]}$ 、 $\text{[math]}$ 点 $\text{[math]}$ 位于对称轴的左侧 $\text{[math]}$ ，设点 $\text{[math]}$ 的纵坐标为 $\text{[math]}$ ．

(1) 求抛物线的解析式；

(2) 当点 $\text{[math]}$ 位于 $\text{[math]}$ 的中点时，求点 $\text{[math]}$ 的坐标；

(3) 点 $\text{[math]}$ 是抛物线上一点，点 $\text{[math]}$ 在整个运动过程中，满足以点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为顶点的四边形是平行四边形时，直接写出 $\text{[math]}$ 的值．

综合题困难

2. 如图，在平面直角坐标系中，经过点 $\text{[math]}$ 的直线AB与y轴交于点 $\text{[math]}$ ．经过原点O的抛物线 $\text{[math]}$ 交直线AB于点A，C，抛物线的顶点为D．

(1) 求抛物线 $\text{[math]}$ 的表达式；

(2) M是线段AB上一点，N是抛物线上一点，当 $\text{[math]}$ 轴且 $\text{[math]}$ 时，求点M的坐标；

(3) P是抛物线上一动点，Q是平面直角坐标系内一点．是否存在以点A，C，P，Q为顶点的四边形是矩形？若存在，直接写出点Q的坐标；若不存在，请说明理由．

综合题困难

3. 如图，已知二次函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ ，与 $\text{[math]}$ 轴分别交于点 $\text{[math]}$ ，点 $\text{[math]}$ .点 $\text{[math]}$ 是直线 $\text{[math]}$ 上方的抛物线上一动点.

(1) 求二次函数 $\text{[math]}$ 的表达式；

(2) 连接 $\text{[math]}$ ， $\text{[math]}$ ，并把 $\text{[math]}$ 沿 $\text{[math]}$ 轴翻折，得到四边形 $\text{[math]}$ .若四边形 $\text{[math]}$ 为菱形，请求出此时点 $\text{[math]}$ 的坐标；

(3) 当点 $\text{[math]}$ 运动到什么位置时，四边形 $\text{[math]}$ 的面积最大？求出此时 $\text{[math]}$ 点的坐标和四边形 $\text{[math]}$ 的最大面积.

综合题普通