1.
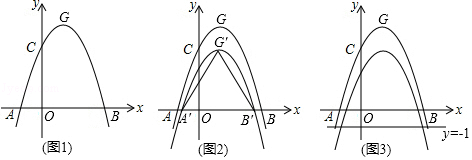
如图1,抛物线C1:y=ax2﹣2ax+c(a<0)与x轴交于A、B两点,与y轴交于点C.已知点A的坐标为(﹣1,0),点O为坐标原点,OC=3OA,抛物线C1的顶点为G.
(1)
求出抛物线C1的解析式,并写出点G的坐标;
(2)
如图2,将抛物线C1向下平移k(k>0)个单位,得到抛物线C2 , 设C2与x轴的交点为A′、B′,顶点为G′,当△A′B′G′是等边三角形时,求k的值:
(3)
在(2)的条件下,如图3,设点M为x轴正半轴上一动点,过点M作x轴的垂线分别交抛物线C1、C2于P、Q两点,试探究在直线y=﹣1上是否存在点N,使得以P、Q、N为顶点的三角形与△AOQ全等,若存在,直接写出点M,N的坐标:若不存在,请说明理由.
【考点】
二次函数图象的几何变换;
待定系数法求二次函数解析式;
全等三角形的判定与性质;
二次函数与一元二次方程的综合应用;
能力提升

