1.
在△ABC中，AB=AC，∠BAC=α，点P是△ABC内一点，且∠PAC+∠PCA= 
，连接PB，试探究PA、PB、PC满足的等量关系．
(1)
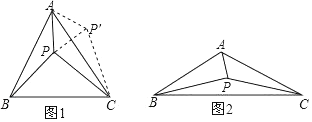
当α=60°时，将△ABP绕点A逆时针旋转60°得到△ACP′，连接PP′，如图1所示．由△ABP≌△ACP′可以证得△APP′是等边三角形，再由∠PAC+∠PCA=30°可得∠APC的大小为度，进而得到△CPP′是直角三角形，这样可以得到PA、PB、PC满足的等量关系为；
(2)
如图2，当α=120°时，参考（1）中的方法，探究PA、PB、PC满足的等量关系，并给出证明；
(3)
PA、PB、PC满足的等量关系为．
【考点】
等腰三角形的性质;
勾股定理;
锐角三角函数的定义;
互余两角三角函数的关系;
旋转的性质;
能力提升
