已知：如图，四边形ABCD是正方形，点E、F分别在BC、CD上，连接AE、EF、AF，且∠DAE＝∠AEF．

0 返回出卷网首页

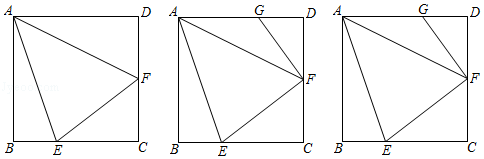
1. 已知：如图，四边形ABCD是正方形，点E、F分别在BC、CD上，连接AE、EF、AF，且∠DAE＝∠AEF．

(1) 求证：EF＝BE+DF；

(2) 线段AF的垂直平分线交AD于点G，连接FG，求证：∠EFG＝90°；

(3) 在（2）的条件下，若tan∠DFG＝ $\text{[math]}$ ，EF＝ $\text{[math]}$ ，求S_△AEF ．

【考点】

全等三角形的判定与性质; 正方形的性质; 解直角三角形;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，在正方形ABCD中，AB=6，E为AC上一点，以AE为直角边构造等腰直角△AEF(点F在AB左侧)，分别延长FB，DE交于点H，DH交线段BC于点M，连结BE。

(1) 求证：△AFB≌△AED

(2) 当AE=4 $\text{[math]}$ 时，求tan∠MBH的值。

(3) 当点H关于直线BE的对称点落在△ABC的边上时，求∠EBC的度数。

(4) 若△BEH与△DEC的面积相等，记△EMC与△ABE的面积分别为S₁ ， S₂ ，则 $\text{[math]}$ 的值为。(直接写出答案)

综合题困难

2. 如图，已知四边形ABCD和四边形DEFG为正方形，点E在线段DE上，点A，D，G在同一直线上，且AD=3，DE=1，连接AC，CG，AE，并延长AE交CG于点H．

(1) 求sin∠EAC的值．

(2) 求线段AH的长．

综合题普通

3. 如图1所示，在正方形ABCD和正方形CGEF中，点B、C、G在同一条直线上，M是线段AE的中点，DM的延长线交EF于点N，连接FM，易证：DM=FM，DM⊥FM（无需写证明过程）

(1) 如图2，当点B、C、F在同一条直线上，DM的延长线交EG于点N，其余条件不变，试探究线段DM与FM有怎样的关系？请写出猜想，并给予证明；

(2) 如图3，当点E、B、C在同一条直线上，DM的延长线交CE的延长线于点N，其余条件不变，探究线段DM与FM有怎样的关系？请直接写出猜想．

综合题普通