1.
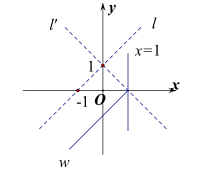
如图,在平面直角坐标系  中,直线
中,直线  轴,且直线
轴,且直线  与抛物线
与抛物线  和
和  轴分别交于点
轴分别交于点  ,点
,点  为抛物线的顶点.若点
为抛物线的顶点.若点  的坐标为
的坐标为  ,点
,点  的横坐标为1.
的横坐标为1.

(1)
线段  的长度等于;
(2)
点
的长度等于;
(2)
点  为线段
为线段  上方抛物线上的一点,过点
上方抛物线上的一点,过点  作
作  的垂线交
的垂线交  于点
于点  ,点
,点  为
为  轴上一点,当
轴上一点,当  的面积最大时,求
的面积最大时,求  的最小值;
(3)
在(2)的条件下,删除抛物线
的最小值;
(3)
在(2)的条件下,删除抛物线  在直线
在直线  左侧部分图象并将右侧部分图象沿直线
左侧部分图象并将右侧部分图象沿直线  翻折,与抛物线在直线
翻折,与抛物线在直线  右侧部分图象组成新的函数
右侧部分图象组成新的函数  的图象.现有平行于
的图象.现有平行于  的直线
的直线  :
:  ,若直线
,若直线  与函数
与函数  的图象有且只有2个交点,求
的图象有且只有2个交点,求  的取值范围(请直接写出
的取值范围(请直接写出  的取值范围,无需解答过程).
的取值范围,无需解答过程).
【考点】
二次函数图象的几何变换;
二次函数y=ax²+bx+c的性质;
能力提升
真题演练