0 返回出卷网首页
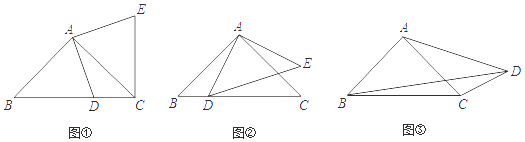
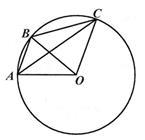
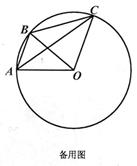
1. 如图，点A，B，C在⊙D上，AB∥0C.

(1) 求证：∠ACB+∠BOC=90°：
(2) 若⊙O的半径为5，AC=8，求BC的长度.
【考点】
全等三角形的判定与性质; 勾股定理; 圆周角定理;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图

(1) 问题：如图①，在Rt△ABC中，AB=AC，D为BC边上一点（不与点B，C重合），将线段AD绕点A逆时针旋转90°得到AE，连接EC，则线段BC，DC，EC之间满足的等量关系式为；
(2) 探索：如图②，在Rt△ABC与Rt△ADE中，AB=AC，AD=AE，将△ADE绕点A旋转，使点D落在BC边上，试探索线段AD，BD，CD之间满足的等量关系，并证明你的结论；
(3) 应用：如图③，在四边形ABCD中，∠ABC=∠ACB=∠ADC=45°．若BD=9，CD=3，求AD的长．
综合题 普通
2. 在正方形ABCD中，连接BD．
(1) 如图1，AE⊥BD于E．直接写出∠BAE的度数．
(2) 如图1，在（1）的条件下，将△AEB以A旋转中心，沿逆时针方向旋转30°后得到△AB′E′，AB′与BD交于M，AE′的延长线与BD交于N．

①依题意补全图1；

②用等式表示线段BM、DN和MN之间的数量关系，并证明．
(3) 如图2，E、F是边BC、CD上的点，△CEF周长是正方形ABCD周长的一半，AE、AF分别与BD交于M、N，写出判断线段BM、DN、MN之间数量关系的思路．（不必写出完整推理过程）
综合题 困难
3. 如图，在△ABC中，AD⊥BC于D，BD=AD，DG=DC，E，F分别是BG，AC的中点．

(1) 求证：DE=DF，DE⊥DF；
(2) 连接EF，若AC=10，求EF的长．

综合题 普通