1.
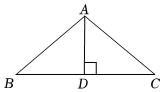
如图,在△ABC中,∠ACB=90°,∠A=45°,CD⊥AB于点D,点P在线段DB上,若AP2-PB2=48,则△PCD的面积为。

【考点】
等腰三角形的性质;
直角三角形的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练