1.
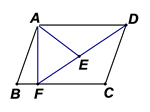
如图,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A、C重合).在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB、AD为邻边作平行四边形ABFD,连接AF.

(1)
根据图①写出线段AF、AE之间存在的等量关系式,并给予证明;
(2)
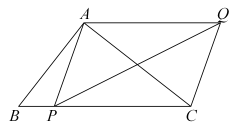
将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请直接
(3)
在图②基础上,将△CED绕点C继续逆时针旋转,请判断(2)间中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,说明理由.
写出线段AF、AE的数量关系 ;
【考点】
勾股定理;
平行四边形的性质;
相似三角形的判定与性质;