1.
定义:从三角形的一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中有一个与原三角形相似,那么我们称这条线段为原三角形的相似线,记此小三角形与原三角形的相似比为k.
(1)
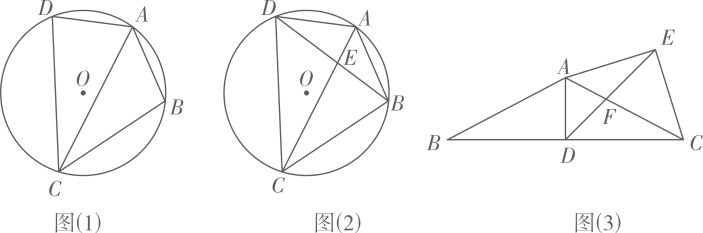
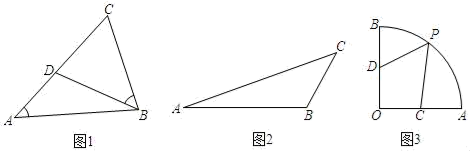
【理解】如图1,△ABC中,已知D是AC边上一点,∠CBD=∠A.求证:BD是△ABC的相似线;
(2)
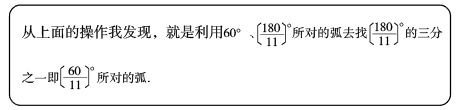
【探究】如图2,△ABC中,AB=4,BC=2,AC=2  .请用尺规作图法在平面内找一点D、使BC是以A、D为其中两个顶点的三角形的相似线,并直接写出k的值,(提醒:保留作图痕迹,在确认无误后用黑色签字笔将作图痕迹描黑)
(3)
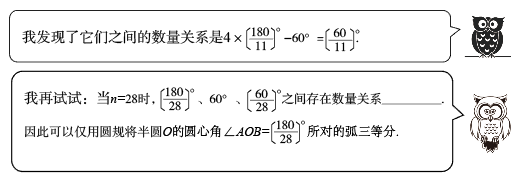
【应用】如图3,扇形AOB中,∠AOB=90°,AO=OB=2,C,D分别是OA,OB的中点,P是弧AB上的一个动点,求PC+2PD的最小值.
.请用尺规作图法在平面内找一点D、使BC是以A、D为其中两个顶点的三角形的相似线,并直接写出k的值,(提醒:保留作图痕迹,在确认无误后用黑色签字笔将作图痕迹描黑)
(3)
【应用】如图3,扇形AOB中,∠AOB=90°,AO=OB=2,C,D分别是OA,OB的中点,P是弧AB上的一个动点,求PC+2PD的最小值.
【考点】
圆的综合题;
相似三角形的判定与性质;
能力提升
真题演练