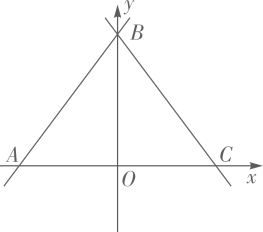
如图，在平面直角坐标系中，点O为坐标原点，直线y= x+4与x轴交于点A，与y轴交于点B，直线BC与x轴交于点C，且点C与点A关于y轴对称。

0 返回出卷网首页

1. 如图，在平面直角坐标系中，点O为坐标原点，直线y= $\text{[math]}$ x+4与x轴交于点A，与y轴交于点B，直线BC与x轴交于点C，且点C与点A关于y轴对称。

(1) 求直线BC的解析式；

(2) 点P为线段AB上一点，点Q为线段BC上一点，BQ=AP，连接PQ，设点P的横坐标为t，△PBO的面积为S（S≠0），求S与t之间的函数关系式（不要求写出自变量t的取值范围）；

(3) 在（2）的条件下，点E在线段0A上，点R在线段BC的延长线上，且点R的纵坐标为 $\text{[math]}$ ，连接PE、BE、AQ，AQ与BE交于点F，∠APE=∠CBE，连接PF，PF的延长线与y轴的负半轴交于点M，连接QM、MR，若tan∠QMR= $\text{[math]}$ ，求直线PM的解析式。

【考点】

待定系数法求一次函数解析式; 锐角三角函数的定义; 二次函数的实际应用-几何问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 在平面直角坐标系中，已知点A（﹣2，0），B（2，0），C（3，5）．

(1) 求过点A，C的直线解析式和过点A，B，C的抛物线的解析式；

(2) 求过点A，B及抛物线的顶点D的⊙P的圆心P的坐标；

(3) 在抛物线上是否存在点Q，使AQ与⊙P相切，若存在请求出Q点坐标．

综合题普通

2. 如图，已知抛物线y=ax²﹣5ax+2（a≠0）与y轴交于点C，与x轴交于点A（1，0）和点B．

(1) 求抛物线的解析式

(2) 求直线BC的解析式

(3) 若点N是抛物线上的动点，过点N作NH⊥x轴，垂足为H，以B，N，H为顶点的三角形是否能够与△OBC相似（排除全等的情况）？若能，请求出所有符合条件的点N的坐标；若不能，请说明理由．

综合题困难

3. 网络销售是一种重要的销售方式．某乡镇农贸公司新开设了一家网店，销售当地农产品．其中一种当地特产在网上试销售，其成本为每千克10元．公司在试销售期间，调查发现，每天销售量 $\text{[math]}$ 与销售单价 $\text{[math]}$ （元）满足如图所示的函数关系（其中 $\text{[math]}$ ）

(1) 求出 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数关系式，并写出自变量的取值范围；

(2) 当 $\text{[math]}$ 时，设每天销售该特产的利润为 $\text{[math]}$ 元，则销售单价 $\text{[math]}$ 为多少元时，每天的销售利润最大?最大利润是多少元?

综合题普通