在正方形ABCD中，对角线BD所在的直线上有两点E、F满足BE=DF，连接AE、AF、CE、CF，如图所示．

0 返回出卷网首页

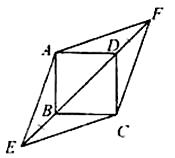
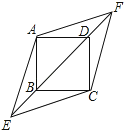
1. 在正方形ABCD中，对角线BD所在的直线上有两点E、F满足BE=DF，连接AE、AF、CE、CF，如图所示．

(1) 求证：△ABE≌△ADF；

(2) 试判断四边形AECF的形状，并说明理由．

【考点】

全等三角形的判定与性质; 菱形的判定; 正方形的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，已知四边形 $\text{[math]}$ 是平行四边形，点 $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 、 $\text{[math]}$ 上的点， $\text{[math]}$ ，并且 $\text{[math]}$ .

求证：

(1) $\text{[math]}$

(2) 四边形 $\text{[math]}$ 是菱形

综合题普通

2. 如图，在平行四边形ABCD中，边AB的垂直平分线交AD于点E，交CB的延长线于点F，连接AF，BE.

(1) 求证：△AGE≌△BGF；

(2) 试判断四边形AFBE的形状，并说明理由．

综合题普通

3. 如图，已知点D在△ABC的BC边上，DE∥AC交AB于E，DF∥AB交AC于F．

(1) 求证：AE=DF；

(2) 若AD平分∠BAC，试判断四边形AEDF的形状，并说明理由．

综合题普通