1.
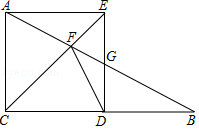
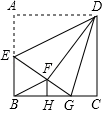
如图,正方形ABCD的边长为4,点M从点D出发,沿射线DC以每秒1个单位长度向右运动,同时点N以相同的速度从A点出发,沿射线AD运动.连结AM、BN,交于点 E.点F为射线CB上的点,且∠MAF=45°,直线AF与直线BN相交于点P.设运动时间为t.

(1)
当0≤t≤4时,求证:AM⊥BN;
(2)
当t=3时,求MF的长;
(3)
当t为何值时,S△PBF:S△ABF=1:5.
【考点】
全等三角形的判定与性质;
正方形的性质;
相似三角形的判定与性质;
锐角三角函数的定义;