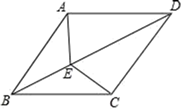
如图，在菱形ABCD中，连结BD、AC交于点O，过点O作于点H，以点O为圆心，OH为半径的半圆交AC于点M． ①求证：DC是⊙O的切线． ②若且，求图中阴影部分的面积． ③在②的条件下，P是线段BD上的一动点，当PD为何值时，的值最小，并求出最小值．

1. 如图，在菱形ABCD中，连结BD、AC交于点O，过点O作 $\text{[math]}$ 于点H，以点O为圆心，OH为半径的半圆交AC于点M．

①求证：DC是⊙O的切线．

②若 $\text{[math]}$ 且 $\text{[math]}$ ，求图中阴影部分的面积．

③在②的条件下，P是线段BD上的一动点，当PD为何值时， $\text{[math]}$ 的值最小，并求出最小值．

【考点】

勾股定理的实际应用-最短路径问题; 菱形的性质; 切线的判定; 几何图形的面积计算-割补法;

【答案】

您现在未登录，无法查看试题答案与解析。登录

证明题困难

1. 如图，四边形 $\text{[math]}$ 是菱形，点 $\text{[math]}$ 、 $\text{[math]}$ 分别在边 $\text{[math]}$ 、 $\text{[math]}$ 的延长线上，且 $\text{[math]}$ .连接 $\text{[math]}$ 、 $\text{[math]}$ .

求证： $\text{[math]}$ .

证明题普通

证明题普通

求证：∠ABF=∠CBE．

证明题普通