1.
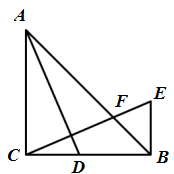
如图,在△ABC中,∠ACB=90°,AC=BC,D为边BC上的一点,连接AD,过点C作AD的垂线,交过点B与边AC平行的直线于点E,CE交边AB于点F.
(1)
求∠EBF的度数;
(2)
求证:△ACD≌△CBE;
(3)
若AD平分∠BAC,判断△BEF的形状,并说明理由.
【考点】
平行线的性质;
全等三角形的判定与性质;
角平分线的性质;
等腰三角形的判定与性质;