1.
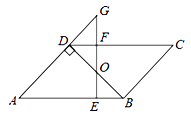
在▱ABCD中,E、F分别是AD、BC上的点,将平行四边形ABCD沿EF所在直线翻折,使点B与点D重合,且点A落在点A′处.

(1)
求证:△A′ED≌△CFD;
(2)
连结BE,若∠EBF=60°,EF=3,求四边形BFDE的面积.
【考点】
全等三角形的判定与性质;
平行四边形的性质;
菱形的判定与性质;
翻折变换(折叠问题);