1.
等腰△ABC 中,AB=AC,∠BAC=120°,点 P 为平面内一点.

(1)
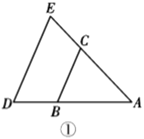
如图 1,当点 P 在边 BC 上时,且满足∠APC=120°,求  的值;
(2)
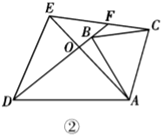
如图 2,当点 P 在△ABC 的外部,且满足∠APC+∠BPC=90°,求证:BP=
的值;
(2)
如图 2,当点 P 在△ABC 的外部,且满足∠APC+∠BPC=90°,求证:BP=  AP;
(3)
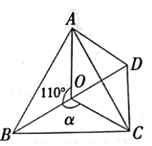
如图 3,点 P 满足∠APC=60°,连接 BP,若 AP=1,PC=3,直接写出BP 的长度.
AP;
(3)
如图 3,点 P 满足∠APC=60°,连接 BP,若 AP=1,PC=3,直接写出BP 的长度.
【考点】
全等三角形的判定与性质;
等腰三角形的性质;
含30°角的直角三角形;
旋转的性质;