已知，在Rt△ABC中，∠ACB＝90°，D是BC边上一点，连接AD，分别以CD和AD为直角边作Rt△CDE和Rt△ADF，使∠DCE＝∠ADF＝90°，点E，F在BC下方，连接EF.

0 返回出卷网首页

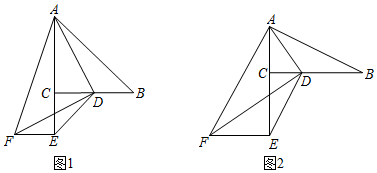
1. 已知，在Rt△ABC中，∠ACB＝90°，D是BC边上一点，连接AD，分别以CD和AD为直角边作Rt△CDE和Rt△ADF，使∠DCE＝∠ADF＝90°，点E，F在BC下方，连接EF.

(1) 如图1，当BC＝AC，CE＝CD，DF＝AD时，

求证：①∠CAD＝∠CDF，

②BD＝EF；

(2) 如图2，当BC＝2AC，CE＝2CD，DF＝2AD时，猜想BD和EF之间的数量关系？并说明理由.

【考点】

全等三角形的判定与性质; 矩形的判定与性质; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图1，在△ABC中，∠ACB=90°，AC=BC，∠EAC=90°，点M为射线AE上任意一点（不与A重合），连接CM，将线段CM绕点C按顺时针方向旋转90°得到线段CN，直线NB分别交直线CM、射线AE于点F、D．

(1) 直接写出∠NDE的度数.

(2) 如图2、图3，当∠EAC为锐角或钝角时，其他条件不变，（1）中的结论是否发生变化？如果不变，选取其中一种情况加以证明；如果变化，请说明理由.

(3) 如图4，若∠EAC=15°，∠ACM=60°，直线CM与AB交于G，BD= $\text{[math]}$ ，其他条件不变，求线段AM的长．

综合题普通

2. 如图，点P在矩形ABCD的对角线AC上，且不与点A，C重合，过点P分别作边AB，AD的平行线，交两组对边于点E，F和G，H．

(1) 求证：△PHC≌△CFP；

(2) 证明四边形PEDH和四边形PFBG都是矩形，并直接写出它们面积之间的关系．

综合题普通

3. 已知，如图1，AD是△ABC的角平分线，且AD=BD，

(1) 求证：△CDA∽△CAB；

(2) 若AD=6，CD=5，求AC的值；

(3) 如图2，延长AD至E，使AE=AB，过E点作EF∥AB，交AC于点F，试探究线段EF与线段AD的大小关系．

综合题普通