1.
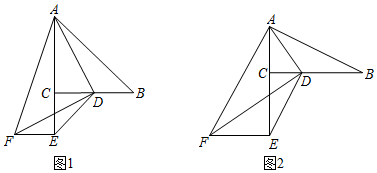
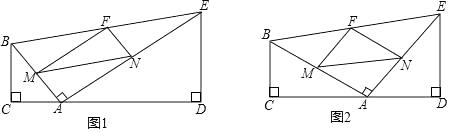
如图①，在四边形BCDE中，BC⊥CD，DE⊥CD，AB⊥AE，垂足分别为C，D，A，BC≠AC，点M，N，F分别为AB，AE，BE的中点，连接MN，MF，NF．
(1)
如图②，当BC=4，DE=5，tan∠FMN=1时，求 
的值；
(2)
若tan∠FMN= 
，BC=4，则可求出图中哪些线段的长？写出解答过程；
(3)
连接CM，DN，CF，DF．试证明△FMC与△DNF全等；
(4)
在（3）的条件下，图中还有哪些其它的全等三角形？请直接写出．
【考点】
全等三角形的判定与性质;
矩形的判定与性质;
相似三角形的判定与性质;
三角形的中位线定理;
直角三角形斜边上的中线;
