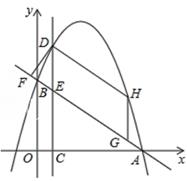
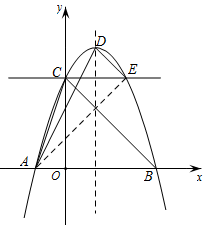
在平面直角坐标系中，抛物线y=﹣x2+bx+c与x轴交于点A，B，与y轴交于点C，直线y=x+4经过A，C两点．

0 返回出卷网首页

1. 在平面直角坐标系中，抛物线y=﹣ $\text{[math]}$ x²+bx+c与x轴交于点A，B，与y轴交于点C，直线y=x+4经过A，C两点．

(1) 求抛物线的解析式；

(2) 在AC上方的抛物线上有一动点P．

①如图1，当点P运动到某位置时，以AP，AO为邻边的平行四边形第四个顶点恰好也在抛物线上，求出此时点P的坐标；

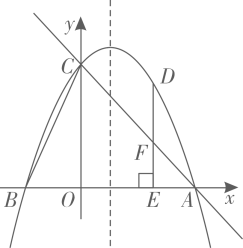
②如图2，过点O，P的直线y=kx交AC于点E，若PE：OE=3：8，求k的值．

【考点】

相似三角形的判定与性质; 二次函数的实际应用-几何问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，在四边形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， P为线段BC上一动点，且和B、C不重合，连结PA，过P作 $\text{[math]}$ 交CD所在直线于E．

(1) 请找出一对相似三角形，并说明理由；

(2) 若点P在线段BC上运动时，点E总在线段CD上，求m的取值范围．

综合题普通

2. △ABC中，BC＝12，高AD＝8，矩形EFGH的一边GH在BC上，顶点E、F分别在AB、AC上，AD与EF交于点M.

(1) 求证： $\text{[math]}$ ；

(2) 设EF＝x，EH＝y，写出y与x之间的函数表达式；

(3) 设矩形EFGH的面积为S，求S与x之间的函数表达式，并写出S的最大值.

综合题困难

3. 如图，有一块三角形土地，它的底边BC＝100m，高AH＝80m．某单位要沿着底边BC修一座底面积是矩形DEFG的大楼．

(1) 求地基的面积y（m²）和边EF的长x（m）的函数关系式；

(2) 当地基的边长EF为多少时地基的面积最大，最大面积是多少？

综合题普通