0 返回出卷网首页
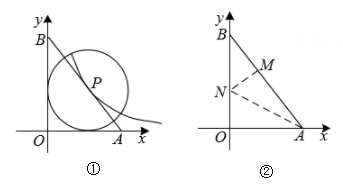
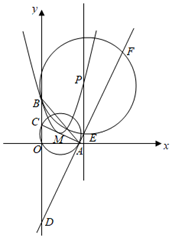
1. 如图，直线l经过点A（4，0），B（0，3）．

(1) 求直线l的函数表达式.
(2) 若圆M的半径为2，圆心M在y轴上，当圆M与直线l相切时，求点M的坐标．
【考点】
待定系数法求一次函数解析式; 切线的性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图，直线y= x+ 与两坐标轴分别交于A、B两点．

(1) 求∠ABO的度数；
(2) 过A的直线l交x轴半轴于C，AB=AC，求直线l的函数解析式．
综合题 普通
2. 如图，在平面内直角坐标系中，直线y=2x+4分别交x轴，y轴于点A，C，点D（m，2）在直线AC上，点B在x轴正半轴上，且OB=3OC，点E是y轴上任意一点，记点E为（0，n）．

(1) 求点D的坐标及直线BC的解析式；
(2) 连结DE，将线段DE绕点D按顺时针旋转90°得线段DG，作正方形DEFG，是否存在n的值，使正方形的顶点F落在△ABC的边上？若存在，求出所有满足条件的n的值；若不存在，说明理由．
(3) 作点E关于AC的对称点E′，当n为何值时，AE′分别与AC，BC，AB垂直？
综合题 困难
3. 直线y=﹣2x+4与x轴交于点A，与y轴交于点B，直线y=kx+b（k，b是常数，k≠0）经过点A，与y轴交于点C，且OC=OA．

(1) 求点A的坐标及k的值；
(2) 点C在x轴的上方，点P在直线y=﹣2x+4上，若PC=PB，求点P的坐标．
综合题 普通