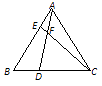1.
在 
中， 
， 
， 
为等边三角形， 
，连接 
， 
为 中点.
(1)
如图1，当 
， 
， 
三点共线时，请画出 
关于点 的中心对称图形，判断 
与 
的位置关系是；
(2)
如图2，当A， ， 三点共线时，问（1）中结论是否成立，若成立，给出证明，若不成立，请说明理由；
(3)
如图2，取 
中点 
，连 
，将 绕点 旋转，直接写出旋转过程中线段 的取值范围是.
【考点】
三角形三边关系;
全等三角形的判定与性质;
等边三角形的性质;
多边形内角与外角;
