0 返回出卷网首页
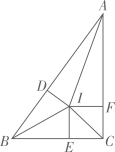
1. 如图，将直角三角形分割成一个正方形和两对全等的直角三角形，在Rt△ABC中，∠ACB=90°，BC=a，AC=b，AB=c；在正方形IECF中，IE=EC=CF=FI=x。

(1) 探究1

小明发现了求正方形边长的方法：由题意可得BD=BE=a-x，AD=AF=b-x，因为AB=BD+AD，所以a-x+b-x=c，解得x= 。
(2) 探究2

小亮发现了另一种求正方形边长的方法：连接IC，利用S△ABC=S△AIB+S△AIC+S△BIC可以得到x与a、b、c的关系．请根据小亮的思路完成他的求解过程。
(3) 探究3

请结合小明和小亮得到的结论验证勾股定理(注：根据比例的基本性质，由 可得ad=bc)。
【考点】
三角形的面积; 勾股定理的证明;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 困难
能力提升
换一批
1. 操作与探索：

在图①～③中，△ABC的面积为a.

(1) 如图①，延长△ABC的边BC到点D，使CD＝BC，连接DA，若△ACD的面积为S1 ， 则S1＝(用含a的式子表示)；
(2) 如图②，延长△ABC的边BC到点D，延长边CA到点E，使CD＝BC，AE＝CA，连接DE，若△DEC的面积为S2 ， 则S2＝(用含a的式子表示)，请说明理由；
(3) 如图③，在图②的基础上延长AB到点F，使BF＝AB，连接FD，FE，得到△DEF，若阴影部分的面积为S3 ， 则S3＝(用含a的式子表示)．
综合题 困难
2. 如图，在Rt△ABC中，∠ACB=90°，CD是AB边上的高，AB=13cm，BC=12cm，AC=5cm．

(1) 求△ABC的面积；
(2) 求CD的长．
综合题 普通
3. 如图，在△ABC中，AB=AC，BG⊥AC于G，DE⊥AB于E，DF⊥AC于F.

(1) 在图（1）中，D是BC边上的中点，判断DE+DF和BG的关系，并说明理由.
(2) 在图（2）中，D是线段BC上的任意一点，DE+DF和BG的关系是否仍然成立？如果成立，证明你的结论；如果不成立，请说明理由.
(3) 在图（3）中，D是线段BC延长线上的点，探究DE、DF与BG的关系.（不要求证明，直接写出结果）
综合题 普通