如图，在△ABC中，∠C＝90°，AB的垂直平分线分别交边BC、AB于点D、E ，联结AD ．

0 返回出卷网首页

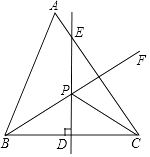
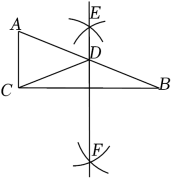
1. 如图，在△ABC中，∠C＝90°，AB的垂直平分线分别交边BC、AB于点D、E ，联结AD ．

(1) 如果∠CAD：∠DAB＝1：2，求∠CAD的度数；

(2) 如果AC＝1，tan∠B＝ $\text{[math]}$ ，求∠CAD的正弦值．

【考点】

线段垂直平分线的性质; 勾股定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图1，我们把对角线互相垂直的四边形叫做垂美四边形．

(1) 概念理解：如图2，在四边形ABCD中，AB=AD，CB=CD，问四边形ABCD是垂美四边形吗？请说明理由．

(2) 性质探究：试探索垂美四边形ABCD两组对边AB，CD与BC，AD之间的数量关系．

猜想结论：（要求用文字语言叙述） $\text{[math]}$

写出证明过程（先画出图形，写出已知、求证）．

(3) 问题解决：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG，GE，已知AC=4，AB=5，求GE长．

综合题困难

2. 如图，在△ABC中，AB=AC，请按要求解答问题.

(1) 作线段AB的垂直平分线，交AB于点D，交AC于点E，连接BE；（尺规作图，不写作法，保留作图痕迹）

(2) 在（1）的基础上，若AC-BC=2，△BCE的周长为8，求AB与BC的长.

综合题普通

3. 如图，在△ABC中，∠A=60°，点D是BC边的中点，DE⊥BC，∠ABC的角平分线BF交DE于△ABC内一点P，连接PC．

(1) 若∠ACP=24°，求∠ABP的度数；

(2) 若∠ACP=m°，∠ABP=n°，请直接写出m，n满足的关系式：．

综合题普通