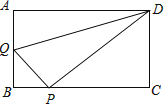
某市政府为了扶贫，鼓励当地农民养殖小龙虾，如图：张叔叔顺着圩梗AN、AM（AN＝3 m ， AM＝10m ， ∠MAN＝45°），用8m长的渔网搭建了一个养殖水域（即四边形ABCD），圩梗边不需要渔网，AB∥CD ， ∠C＝90°．设BC＝xm ，四边形ABCD面积为S（m2）．

0 返回出卷网首页

1. 某市政府为了扶贫，鼓励当地农民养殖小龙虾，如图：张叔叔顺着圩梗AN、AM（AN＝3 $\text{[math]}$ m ， AM＝10m ， ∠MAN＝45°），用8m长的渔网搭建了一个养殖水域（即四边形ABCD），圩梗边不需要渔网，AB∥CD ， ∠C＝90°．设BC＝xm ，四边形ABCD面积为S（m²）．

(1) 求出S关于x的函数表达式及x的取值范围；

(2) x为何值时，围成的养殖水域面积最大？最大面积是多少？

【考点】

二次函数的最值; 矩形的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 一个足球被从地面向上踢出，它距地面高度y（m）可以用二次函数y=﹣4.9x²+19.6x刻画，其中x（s）表示足球被踢出后经过的时间．

(1) 解方程﹣4.9x²+19.6x=0，并说明其根的实际意义；

(2) 求经过多长时间，足球到达它的最高点？最高点的高度是多少？

综合题普通

2. 已知函数y=-x²+bx+c（b，c为常数）的图象经过点（0，﹣3），（﹣6，﹣3）．

(1) 求b，c的值．

(2) 当﹣4≤x≤0时，求y的最大值．

(3) 当m≤x≤0时，若y的最大值与最小值之和为2，求m的值．

综合题普通

3. 已知函数 $\text{[math]}$ 为常数）的图象经过点 $\text{[math]}$ ．

(1) 求 $\text{[math]}$ 满足的关系式；

(2) 设该函数图象的顶点坐标是 $\text{[math]}$ ，当 $\text{[math]}$ 的值变化时，求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数解析式；

(3) 设该函数的图象不经过第三象限，当-5 $\text{[math]}$ 时，函数的最大值与最小值之差为16，求 $\text{[math]}$ 的值．

综合题普通