如图1，抛物线y＝﹣x2+mx+n交x轴于点A(﹣2，0)和点B，交y轴于点C(0，2).

0 返回出卷网首页

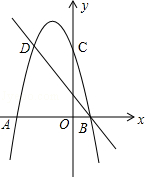
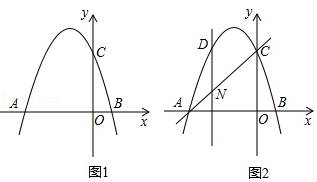
1. 如图1，抛物线y＝﹣x²+mx+n交x轴于点A(﹣2，0)和点B，交y轴于点C(0，2).

(1) 求抛物线的函数表达式；

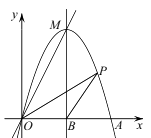
(2) 若点M在抛物线上，且S_△_AOM＝2S_△_BOC ，求点M的坐标；

(3) 如图2，设点N是线段AC上的一动点，作DN⊥x轴，交抛物线于点D，求线段DN长度的最大值.

【考点】

待定系数法求二次函数解析式; 二次函数与一次函数的综合应用; 二次函数图象上点的坐标特征;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，抛物线 $\text{[math]}$ .与x轴交于A，B两点，与y轴交于 $\text{[math]}$ 直线 $\text{[math]}$ 经过点A且与抛物线交于另一点D.

(1) 求抛物线的解析式；

(2) 若P是位于直线 $\text{[math]}$ 上方的抛物线上的一个动点，连接 $\text{[math]}$ ，求 $\text{[math]}$ 的面积的最大值.

综合题普通

2. 如图，二次函数y=﹣x²+ $\text{[math]}$ x+4与x轴交于A、B两点，与y轴交于点C，点P从点O出发沿OA以每秒1个单位长度的速度向点A运动，到达点A后立刻在以原来的速度沿AO返回；点Q从点A出发沿AC以每秒1个单位长度的速度向点C匀速运动，过点Q作QD⊥x轴，垂足为D．点P、Q同时出发，当点Q到达点C时停止运动，点P也随之停止．设点P，Q的运动时间为t（t≥0）．

(1) 当点P从点O向点A运动的过程中，求△QPA面积S与t的函数关系式；

(2) 当线段PQ与抛物线的对称轴没有公共点时，请直接写出t的取值范围；

(3) 当t为何值时，以P、D、Q为顶点的三角形与△OBC相似；

(4) 如图2：FE保持垂直平分PQ，且交PQ于点F，交折线QC﹣CO﹣OP于点E，在整个运动过程中，请你直接写出点E所经过的路径长．

综合题困难

3. 如图，二次函数的图象与x轴交于A（﹣3，0）和B（1，0）两点，交y轴于点C（0，3），点C、D是二次函数图象上的一对对称点，一次函数的图象过点B、D．

(1) 请直接写出D点的坐标．

(2) 求二次函数的解析式．

(3) 根据图象直接写出使一次函数值大于二次函数值的x的取值范围．

综合题普通