已知：四边形ABCD是平行四边形，点O是对角线AC、BD的交点，EF过点O且与AB、CD分别相交于点E、F ，连接EC、AF ．

0 返回出卷网首页

1. 已知：四边形ABCD是平行四边形，点O是对角线AC、BD的交点，EF过点O且与AB、CD分别相交于点E、F ，连接EC、AF ．

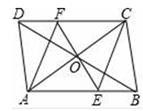
(1) 求证：DF＝EB；

(2) AF与图中哪条线段平行？请指出，并说明理由．

【考点】

三角形全等及其性质; 三角形全等的判定; 平行四边形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. ∆ABC中，点D在直线AB上.点E在平面内，点F在BC的延长线上，∠E=∠BDC，AE=CD，∠EAB+∠DCF=180º．

(1) 如图①，求证AD+BC=BE；

(2) 如图②、图③，请分别写出线段AD，BC，BE之间的数量关系，不需要证明；

(3) 若BE⊥BC，tan∠BCD= $\text{[math]}$ ，CD=10，则AD=．

综合题困难

2. 如图，在▱ABCD中，点E，F在对角线AC上，且AE=CF．求证：

(2) 四边形DEBF是平行四边形．

综合题普通

3. 不在射线 $\text{[math]}$ 上的点P是边长为2的正方形 $\text{[math]}$ 外一点，且满足 $\text{[math]}$ ，以 $\text{[math]}$ ， $\text{[math]}$ 为邻边作 $\text{[math]}$ ．

(1) 如图，若点P在射线 $\text{[math]}$ 上，请用尺规补全图形；

(2) 若点P不在射线 $\text{[math]}$ 上，且在AB的左侧，求 $\text{[math]}$ 的度数；

(3) 设 $\text{[math]}$ 与 $\text{[math]}$ 交点为O，当 $\text{[math]}$ 的面积最大时，求 $\text{[math]}$ 的值．

综合题普通