0 返回出卷网首页
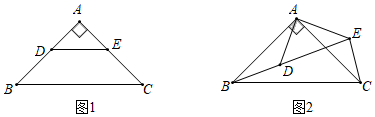
1. 把两个等腰直角△ABC和△ADE按如图1所示的位置摆放，将△ADE绕点A按逆时针方向旋转，如图2，连接BD ， EC ， 设旋转角为α（0°＜α＜360°）

(1) 当DE⊥AC时，AD与BC的位置关系是，AE与BC的位置关系是；
(2) 如图2，当点D在线段BE上时，求∠BEC的度数；
(3) 当旋转角α＝时，△ABD的面积最大．
【考点】
全等三角形的判定与性质; 旋转的性质; 等腰直角三角形;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 困难
能力提升
真题演练
换一批
1. 如图1是实验室中的一种摆动装置，BC在地面上，支架ABC是底边为BC的等腰直角三角形，摆动臂AD可绕点A旋转，摆动臂DM可绕点D旋转，AD＝30，DM＝10.

(1) 在旋转过程中，

①当A，D，M三点在同一直线上时，求AM的长.

②当A，D，M三点为同一直角三角形的顶点时，求AM的长.
(2) 若摆动臂AD顺时针旋转90°，点D的位置由△ABC外的点D1转到其内的点D2处，连结D1D2 ， 如图2，此时∠AD2C＝135°，CD2＝60，求BD2的长.
综合题 普通
2. 如图1，已知∠ACB＝90°，AC＝BC，BD⊥DE，AE⊥DE，垂足分别为D、E.（这几何模型具备“一线三直角”）如下图1：

(1) ①请你证明：△ACE≌△CBD；②若AE＝3，BD＝5，求DE的长；
(2) 迁移：如图2：在等腰Rt△ABC中，且∠C＝90°，CD＝2，BD＝3，D、E分别是边BC，AC上的点，将DE绕点D顺时针旋转90°，点E刚好落在边AB上的点F处，则CE＝.（不要求写过程）
综合题 普通
3. 已知△ABC和△ADE都是等腰直角三角形，∠ACB＝∠ADE＝90°，点F为BE中点，连结DF，CF．

(1) 如图1，点D在AC上，请你判断此时线段DF，CF的关系，并证明你的判断；
(2) 如图2，在（1）的条件下将△ADE绕点A顺时针旋转45度时，若AD＝DE＝2，AB＝6，求此时线段CF的长．
综合题 困难