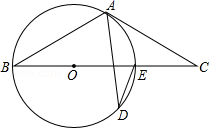
如图，在△ABC中，∠BAC=30°，以AB为直径的⊙O经过点C．过点C作⊙O的切线交AB的延长线于点P．点D为圆上一点，且 = ，弦AD的延长线交切线PC于点E，连接BC．

如图，在△ABC中，∠BAC=30°，以AB为直径的⊙O经过点C．过点C作⊙O的切线交AB的延长线于点P．点D为圆上一点，且 $\text{[math]}$ = $\text{[math]}$ ，弦AD的延长线交切线PC于点E，连接BC．

(1) 判断OB和BP的数量关系，并说明理由；

(2) 若⊙O的半径为2，求AE的长．

【考点】

含30°角的直角三角形; 圆心角、弧、弦的关系; 圆周角定理; 切线的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图1， $\text{[math]}$ 是 $\text{[math]}$ 的切线，切点为点 $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，点 $\text{[math]}$ 是优弧 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ．

综合题普通

综合题普通

综合题普通