1.
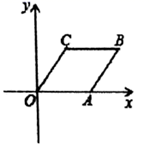
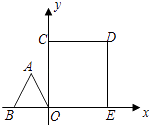
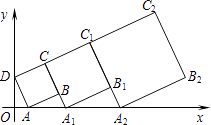
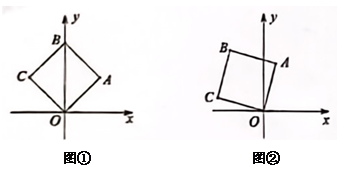
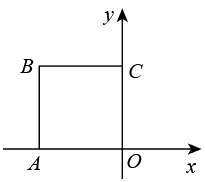
如图,在平面直角坐标系中,点A和点B分别在x轴和y轴的正半轴上,OA=OB=a,以线段AB为边在第一象限作正方形ABCD,CD的延长线交x轴于点E,再以CE为边作第二个正方形ECGF,…,依此方法作下去,则第n个正方形的边长是 .

【考点】
坐标与图形性质;
正方形的性质;
等腰直角三角形;
基础巩固
能力提升
变式训练
拓展培优
真题演练