1.
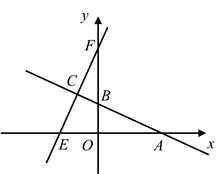
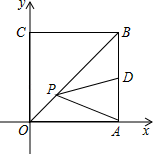
在平面直角坐标系中,点O为原点,点A的坐标为(﹣6,0).如图1,正方形OBCD的顶点B在x轴的负半轴上,点C在第二象限.现将正方形OBCD绕点O顺时针旋转角α得到正方形OEFG.

(1)
如图2,若α=60°,OE=OA,求直线EF的函数表达式.
(2)
若α为锐角,tanα=  ,当AE取得最小值时,求正方形OEFG的面积.
(3)
当正方形OEFG的顶点F落在y轴上时,直线AE与直线FG相交于点P,△OEP的其中两边之比能否为
,当AE取得最小值时,求正方形OEFG的面积.
(3)
当正方形OEFG的顶点F落在y轴上时,直线AE与直线FG相交于点P,△OEP的其中两边之比能否为  :1?若能,求点P的坐标;若不能,试说明理由
:1?若能,求点P的坐标;若不能,试说明理由
【考点】
待定系数法求一次函数解析式;
正方形的性质;