0 返回出卷网首页
1.

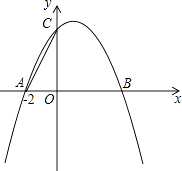
如图，已知抛物线y=ax2+bx+4与x轴交于A（﹣2，0）、B两点，与y轴交于C点，其对称轴为直线x=1．

(1) 直接写出抛物线的解析式：；
(2) 把线段AC沿x轴向右平移，设平移后A、C的对应点分别为A′、C′，当C′落在抛物线上时，求A′、C′的坐标；
(3) 除（2）中的点A′、C′外，在x轴和抛物线上是否还分别存在点E、F，使得以A、C、E、F为顶点的四边形为平行四边形？若存在，求出E、F的坐标；若不存在，请说明理由．
【考点】
待定系数法求二次函数解析式; 平行四边形的性质; 坐标与图形变化﹣平移; 二次函数图象上点的坐标特征; 二次函数-动态几何问题;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 困难
能力提升
换一批
1. 在如图所示的平面直角坐标系中，抛物线y=﹣ x2+bx+c过点A（0，4）和C（8，0），点P（t，0）是线段OC上的动点，PB⊥PA，且PB= PA，过点B作x轴的垂线，过点A作y轴的垂线，两直线相交于点D；

(1) 求抛物线的解析式；
(2) 当t为何值时，点D落在抛物线上；
(3) 是否存在t，使得以A，B，D为顶点的三角形与△AOP相似？若存在，求此时t的值；若不存在，请说明理由．
综合题 困难
2. 已知抛物线 y = ax2+ bx+2 经过点 A （-2，0）．
(1) b＝（用含 a 的代数式表示）；
(2) 若抛物线 y = ax2+ bx+2 与 x 轴的另一交点为 B，且 AB＝3．求 a 的值；
(3) 在（2）的条件下，当 a 为整数时，记抛物线的顶点为 M．现将该抛物线进行平移，使平移后的抛物线的顶点在直线 OM 上运动．当平移后的抛物线恰好经过原点时，求平移后的抛物线的解析式．
综合题 普通
3. 如图，抛物线y=﹣x2+bx+c经过A（﹣1，0），B（3，0）两点，且与y轴交于点C，点D是抛物线的顶点，抛物线的对称轴DE交x轴于点E，连接BD．

(1) 求经过A，B，C三点的抛物线的函数表达式；
(2) 点P是线段BD上一点，当PE=PC时，求点P的坐标；
(3) 在（2）的条件下，过点P作PF⊥x轴于点F，G为抛物线上一动点，M为x轴上一动点，N为直线PF上一动点，当以F、M、N、G为顶点的四边形是正方形时，请求出点M的坐标．
综合题 困难