如图，抛物线y=﹣x2+bx+c经过A（﹣1，0），B（3，0）两点，且与y轴交于点C，点D是抛物线的顶点，抛物线的对称轴DE交x轴于点E，连接BD．

0 返回出卷网首页

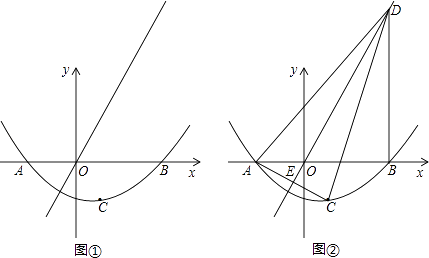
1. 如图，抛物线y=﹣x²+bx+c经过A（﹣1，0），B（3，0）两点，且与y轴交于点C，点D是抛物线的顶点，抛物线的对称轴DE交x轴于点E，连接BD．

(1) 求经过A，B，C三点的抛物线的函数表达式；

(2) 点P是线段BD上一点，当PE=PC时，求点P的坐标；

(3) 在（2）的条件下，过点P作PF⊥x轴于点F，G为抛物线上一动点，M为x轴上一动点，N为直线PF上一动点，当以F、M、N、G为顶点的四边形是正方形时，请求出点M的坐标．

【考点】

待定系数法求二次函数解析式; 二次函数图象上点的坐标特征; 二次函数-动态几何问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 在如图所示的平面直角坐标系中，抛物线y=﹣ $\text{[math]}$ x²+bx+c过点A（0，4）和C（8，0），点P（t，0）是线段OC上的动点，PB⊥PA，且PB= $\text{[math]}$ PA，过点B作x轴的垂线，过点A作y轴的垂线，两直线相交于点D；

(1) 求抛物线的解析式；

(2) 当t为何值时，点D落在抛物线上；

(3) 是否存在t，使得以A，B，D为顶点的三角形与△AOP相似？若存在，求此时t的值；若不存在，请说明理由．

综合题困难

2. 已知抛物线 y = ax²+ bx+2 经过点 A （-2，0）．

(1) b＝（用含 a 的代数式表示）；

(2) 若抛物线 y = ax²+ bx+2 与 x 轴的另一交点为 B，且 AB＝3．求 a 的值；

(3) 在（2）的条件下，当 a 为整数时，记抛物线的顶点为 M．现将该抛物线进行平移，使平移后的抛物线的顶点在直线 OM 上运动．当平移后的抛物线恰好经过原点时，求平移后的抛物线的解析式．

综合题普通

3. 如图①，若二次函数y= $\text{[math]}$ x²+bx+c的图象与x轴交于A（﹣2，0），B（3，0）两点，点A关于正比例函数y= $\text{[math]}$ x的图象的对称点为C．

(1) 求b、c的值；

(2) 证明：点C在所求的二次函数的图象上；

(3) 如图②，过点B作DB⊥x轴交正比例函数y= $\text{[math]}$ x的图象于点D，连结AC，交正比例函数y= $\text{[math]}$ x的图象于点E，连结AD、CD．如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动，同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动．当其中一个点到达终点时，另一个点随之停止运动，连结PQ、QE、PE．设运动时间为t秒，是否存在某一时刻，使PE平分∠APQ，同时QE平分∠PQC？若存在，求出t的值；若不存在，请说明理由．

综合题普通