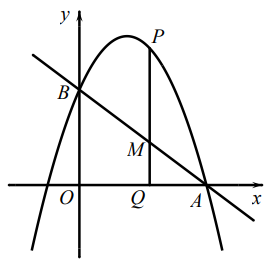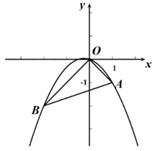
如图在平面直角坐标系中顶点为点M的抛物线是由抛物线向右平移1个单位得到的，它与y轴负半轴交于点A，点B在抛物线上，且横坐标为3.

0 返回出卷网首页

1. 如图在平面直角坐标系中顶点为点M的抛物线是由抛物线 $\text{[math]}$ 向右平移1个单位得到的，它与y轴负半轴交于点A，点B在抛物线上，且横坐标为3.

(1) 写出以M为顶点的抛物线解析式.

(2) 连接AB，AM，BM，求 $\text{[math]}$ ；

(3) 点P是顶点为M的抛物线上一点，且位于对称轴的右侧，设PO与x正半轴的夹角为 $\text{[math]}$ ，当 $\text{[math]}$ 时，求点P坐标.

【考点】

二次函数图象的几何变换; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，抛物线y＝ax²+c（a≠0）与y轴交于点A，与x轴交于B，C两点（点C在x轴正半轴上），△ABC为等腰直角三角形，且面积为4，现将抛物线沿BA方向平移，平移后的抛物线过点C时，与x轴的另一交点为E，其顶点为F.

(1) 求a、c的值；

(2) 连接OF，试判断△OEF是否为等腰三角形，并说明理由.

综合题困难

2. 如图，抛物线L：y＝﹣x²＋bx＋c与x轴交于点A（﹣1，0），且抛物线过点B（﹣4，﹣3），顶点为C.

(1) 求抛物线L的函数表达式及顶点C的坐标；

(2) 抛物线L′与抛物线L关于原点O对称，抛物线L′与x轴交于点M、N（点M在点N的左侧），在点N右侧的抛物线L′上是否存在一点P，作PD⊥x轴于点D，使得以点P，M，D为顶点的三角形与△ABC相似？若存在，求出P点坐标；若不存在，请说明理由.

综合题困难

3. 如图，二次函数 $\text{[math]}$ 的图像经过 $\text{[math]}$ 的三个顶点，其中 $\text{[math]}$ ， $\text{[math]}$

(1) 求点A，B的坐标；

(2) 在第三象限存在点C，使以 $\text{[math]}$ 为顶点的四边形是平行四边形，求满足条件的点C的坐标；

(3) 在（2）的条件下，能否将抛物线 $\text{[math]}$ 平移后经过 $\text{[math]}$ 两点，若能求出平移后经过 $\text{[math]}$ 两点的拋物线的表达式，并写出平移过程.若不能，请说明理由.

综合题困难