如图，在平面直角坐标系中，抛物线与x轴交于点 A(4，0)，与 y 轴交于点 B(0，3)．

0 返回出卷网首页

1. 如图，在平面直角坐标系中，抛物线 $\text{[math]}$ 与x轴交于点 A(4，0)，与 y 轴交于点 B(0，3)．

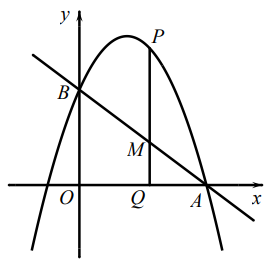
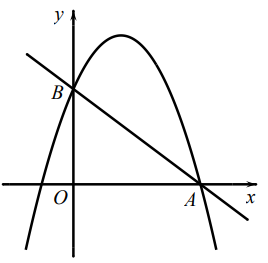
(1) 求抛物线的函数表达式；

(2) 点 P为直线AB上方抛物线上一动点，过点P作 PQ⊥x 轴于点Q，交 AB于点 M，求 $\text{[math]}$ 的最大值及此时点 P 的坐标；

(3) 在（2）的条件下，点 P' 与点P关于抛物线 $\text{[math]}$ 的对称轴对称．将抛物线 $\text{[math]}$ 向右平移，使新抛物线的对称轴l经过点A．点 C 在新抛物线上，点D在l上，直接写出所有使得以点 A、P'、C、D为顶点的四边形是平行四边形的点 D 的坐标，并把求其中一个点D的坐标的过程写出来．

【考点】

二次函数图象的几何变换; 二次函数的最值; 平行四边形的判定与性质; 相似三角形的判定与性质; 二次函数-动态几何问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 已知抛物线 $\text{[math]}$ 与x轴交于A、B两点（A点在B点左侧），与y轴交于点C ，且 $\text{[math]}$ ，该抛物线的对称轴为直线 $\text{[math]}$ ．

(1) 求该抛物线的解析式；

(2) 如图1，E为直线 $\text{[math]}$ 下方抛物线上一点，过点E作 $\text{[math]}$ 轴交直线 $\text{[math]}$ 于点F ，求 $\text{[math]}$ 的最大值及此时点E的坐标；

(3) 将该抛物线沿射线 $\text{[math]}$ 方向平移 $\text{[math]}$ 个单位，得到新的抛物线 $\text{[math]}$ ， M为 $\text{[math]}$ 与y轴的交点，N为新抛物线 $\text{[math]}$ 对称轴上一点，点C平移后的对应点为Q ，平面内是否存在点P ，使得以M、N、P、Q为顶点的四边形为矩形，若存在请写出所有点P的坐标，并写出其中一种情况的过程；若不存在请说明理由．

综合题困难

2. 如图1， $\text{[math]}$ 的面积为1，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ 分别在边 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 上， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .设 $\text{[math]}$ ，图形 $\text{[math]}$ 的面积为 $\text{[math]}$ .

(1) 如图2，当点 $\text{[math]}$ 和点 $\text{[math]}$ 重合时，求 $\text{[math]}$ 与 $\text{[math]}$ 的值；

(2) 如图1，当点 $\text{[math]}$ 和点 $\text{[math]}$ 不重合时，求 $\text{[math]}$ 的最大值.

综合题困难

3. 如图，在▱ABCD中，点E、F分别在边AD、BC上，且∠ABE＝∠CDF．

(1) 探究四边形BEDF的形状，并说明理由；

(2) 连接AC，分别交BE、DF于点G、H，连接BD交AC于点O．若 $\text{[math]}$ ， AE＝4，求BC的长．

综合题普通