1.
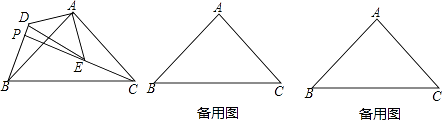
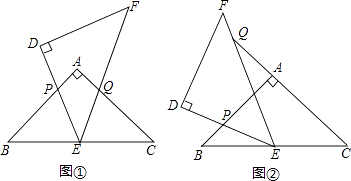
如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.

(1)
如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
(2)
如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=a,CQ=  时,P、Q两点间的距离 (用含a的代数式表示).
时,P、Q两点间的距离 (用含a的代数式表示).
【考点】
全等三角形的判定与性质;
相似三角形的判定与性质;
旋转的性质;
等腰直角三角形;
能力提升
真题演练