抛物线y=﹣x2平移后的位置如图所示，点A，B坐标分别为（﹣1，0）、（3，0），设平移后的抛物线与y轴交于点C，其顶点为D．

0 返回出卷网首页

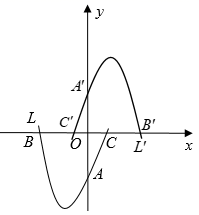
1. 抛物线y=﹣x²平移后的位置如图所示，点A，B坐标分别为（﹣1，0）、（3，0），设平移后的抛物线与y轴交于点C，其顶点为D．

(1) 求平移后的抛物线的解析式和点D的坐标；

(2) ∠ACB和∠ABD是否相等？请证明你的结论；

(3) 点P在平移后的抛物线的对称轴上，且△CDP与△ABC相似，求点P的坐标．

【考点】

二次函数图象的几何变换; 勾股定理的逆定理; 相似三角形的性质; 同角三角函数的关系; 二次函数y=ax²+bx+c与二次函数y=a（x-h）²+k的转化;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 在平面直角坐标系xOy中，抛物线y＝ax²﹣4ax+3a的最高点的纵坐标是2.

(1) 求抛物线的对称轴及抛物线的表达式；

(2) 将抛物线在1≤x≤4之间的部分记为图象G₁ ，将图象G₁沿直线x＝1翻折，翻折后的图象记为G₂ ，图象G₁和G₂组成图象G.过（0，b）作与y轴垂直的直线l，当直线l和图象G只有两个公共点时，将这两个公共点分别记为P₁（x₁ ， y₁），P（x₂ ， y₂），求b的取值范围和x₁+x₂的值.

综合题普通

2. 如图，已知抛物线L：y＝x²+bx﹣4交y轴于点A，交x轴于点B(﹣4，0)、C.抛物线L关于原点O对称的抛物线为 $\text{[math]}$ ，点A在抛物线 $\text{[math]}$ 上的对应点为A'.

(1) 求抛物线 $\text{[math]}$ 的函数表达式；

(2) 过点 $\text{[math]}$ 作平行于x轴的直线l，点P是抛物线 $\text{[math]}$ 上一动点，过点P作PQ⊥l于Q，连接 $\text{[math]}$ .若 $\text{[math]}$ ，求点P的坐标.

综合题普通

3. 如图，抛物线L：y＝﹣x²＋bx＋c与x轴交于点A（﹣1，0），且抛物线过点B（﹣4，﹣3），顶点为C.

(1) 求抛物线L的函数表达式及顶点C的坐标；

(2) 抛物线L′与抛物线L关于原点O对称，抛物线L′与x轴交于点M、N（点M在点N的左侧），在点N右侧的抛物线L′上是否存在一点P，作PD⊥x轴于点D，使得以点P，M，D为顶点的三角形与△ABC相似？若存在，求出P点坐标；若不存在，请说明理由.

综合题困难