如图，在△ABC中，∠ABC=90°，将△ABC绕点C顺时针旋转得到△DEC，连接AD，BE，延长BE交AD于点F．

0 返回出卷网首页

1. 如图，在△ABC中，∠ABC=90°，将△ABC绕点C顺时针旋转得到△DEC，连接AD，BE，延长BE交AD于点F．

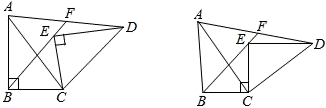
(1) 求证：∠DEF=∠ABF；

(2) 求证：F为AD的中点；

(3) 若AB=8，AC=10，且EC⊥BC，求EF的长．

【考点】

全等三角形的判定与性质; 勾股定理; 旋转的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ $\text{[math]}$ 是斜边 $\text{[math]}$ 上两点，且 $\text{[math]}$ 将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转90°后，得到 $\text{[math]}$ 连接 $\text{[math]}$

(1) 求证： △AED≌△AEF

(2) 猜想线段BE，ED，DC之间的关系，并证明

综合题普通

(1) 如图①所示，将 $\text{[math]}$ 绕顶点 $\text{[math]}$ 按逆时针方向旋转 $\text{[math]}$ 角，得到 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别与 $\text{[math]}$ 、 $\text{[math]}$ 交于点 $\text{[math]}$ 、 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ．求证： $\text{[math]}$ ；

(2) 如图②所示， $\text{[math]}$ 和 $\text{[math]}$ 是全等的等腰直角三角形， $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 、 $\text{[math]}$ 分别交于点 $\text{[math]}$ 、 $\text{[math]}$ ，请说明 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系．

综合题困难

3. 如图，在直角坐标系中，点A在x轴上，且A(4，0)，点B在y轴上，且B(0，4).

(1) 求线段AB的长；

(2) 若点E在线段AB上，OE⊥OF，且OE=OF，求AE+AF的值；

(3) 在（2）的条件下，过O作OM⊥EF，交AB于M，试确定线段BE、EM、AM之间的数量关系?并证明你的结论.

综合题普通