1.
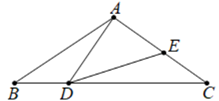
已知:如图,△ABC中,AB=AC,D,E分别是边BC,AC上的点.且BD=EC,∠ADE=∠B.
(1)
求证:AD=DE.
(2)
若∠ADE=40°,求∠ADB的度数.
【考点】
三角形内角和定理;
全等三角形的判定与性质;
等腰三角形的性质;
能力提升
真题演练
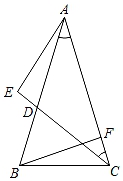
 图9
图9